Compiler Syntax Analysis

Syntax analysis is the second phase of a compiler.

• Take a stream of tokens from the lexer as input.
• Analyze the structure of the tokens.
• Detect syntax errors.
• Out put a parsing tree to present the structure.

Use context-free grammar (CFG) for analysis.

Context-free grammar (CFG)

[!question]+ Why CFG?

• CFG is more powerful than regular expressions.
• CFGs are not the most powerful formal language (see Chomsky hierarchy),
• but CFGs are enough to describe the structures for most of the languages.

CFG

+ Context free grammar

A Context free grammar is a $4-tuple(N,T,R,S)$, where

• $N$ is a finite set called Variables
• $T$ is a finite set, disjoint from $N$, called the terminals,
• $R$ is a finite set of production rules, with each rule being a variable $v$ and a string $s$ of variables and terminals in the form $v\to s$, and
• $S\in N$ is the start variable.

The production rules are same as the rules in the regular definition.

We can use the rules to derive the strings in a context-free language.

Terminals are the symbols which cannot produce more symbols. In a compiler, they are tokens.

Variables only exists when the production is unfinished. They are not symbols in the alphabet, neither tokens. Thus, they are not in the strings of the language.

CFG example

For example,

• $N=\{E\}$ Variables
• $T=\{+,\ast ,(,),-,id\}$ Terminals
• $R=\{E\to E+E,E\to E\ast E,E\to (E),E\to -E,E\to id\}$
• $S=E$

The production rules can also be "combined" and rewritten as

• $R=\{E\to E+E|E\ast E|(E)|(E)|-E|id\}$ The symbol "|" is same as it is in regular expressions, meaning that there are multiple options.

The rules can be combined only if the LHS are the same. Sometimes the set of production rules is enough to define a grammar because

• Variables can be obtained by looking at the LHS of each production rule,
• Terminals are the symbols on the RHS of the rules excluding the variables, and
• The start symbol is usually denoted by $E$.

Then, the above grammar can be

$$E\to E+E|E\ast E|(E)|-E|id$$

Derivations

+ Derivations

Given a grammar $G$, we can generate strings in the language $L(G)$ by using a derivation. A derivation (informally) is a procedure to apply the production rules from the start symbol to a string which only contains terminals.

Each production is denoted by $\Rightarrow$.

For example, given the grammar

$$E\to E+E|E\ast E|(E)|-E|id$$

left-most derivation, meaning that each iteration we replace the left most nonterminal.

Derivation	Rule Used
$$E$$	Start symbol
$$E \Rightarrow E + E$$	Rule 1
$$E \Rightarrow id + E$$	Rule 5
$$E \Rightarrow id + E * E$$	Rule 2
$$E \Rightarrow id + id * E$$	Rule 5
$$E \Rightarrow id + id * id$$	Rule 5

Similarly, the right-most derivation replaces the right most nonterminal in each iteration.

Derivation	Rule Used
$$E$$	Start symbol
$$E \Rightarrow E + E$$	Rule 1
$$E \Rightarrow E + E * E$$	Rule 2
$$E \Rightarrow E + E * id$$	Rule 5
$$E \Rightarrow E + id * id$$	Rule 5
$$E \Rightarrow id + id * id$$	Rule 5

Each sequence of nonterminals and tokens that we derive at each step is called a sentential form.

• The last sentential form only contains tokens and is called a sentence, which is a syntactically correct string in the programming language.

• If $w$ is a sentence and $S$ is the start symbol, we can write

  $$S\stackrel{\ast }{\Rightarrow }w$$

• $\stackrel{\ast }{\Rightarrow }$ means derive in zero or more steps. It also means the RHS is derivable by the LHS.

• From the above example,

  $$E\stackrel{\ast }{\Rightarrow }id+id\ast id$$

Ambiguous

The grammar $G$ is ambiguous if there is a sentence in $L(G)$ from which it is possible to construct multiple parse trees (using any type of derivation).

[!abstract]+ Some properties

• Each derivation (left-most, right-most, or otherwise) corresponds to exactly one parse tree, whether the grammar is ambiguous or not.
• 每个推导（无论是最左推导、最右推导或其他推导）对应唯一一个语法树，无论语法是否有歧义。
• Each parse tree corresponds to multiple derivations, whether the grammar is ambiguous or not. 每个语法树可以对应多个推导，无论语法是否有歧义。
• Each parse tree corresponds to exactly one left-most derivation and exactly one right-most derivation, whether the grammar is ambiguous or not. 每个语法树对应唯一的最左推导和最右推导。
• All derivations of the same sentence correspond to the same parse tree if the grammar is not ambiguous. 如果语法没有歧义，同一语句的所有推导对应相同的语法树。
• Multiple derivations of the same sentence may not correspond to the same parse tree if the grammar is ambiguous. 如果语法没有歧义，同一语句的所有推导对应相同的语法树。
• In general, deciding a grammar is ambiguous or not is undecidable, or uncomputable (like the halting problem).
• 一般来说，判断一个语法是否有歧义是不可判定或不可计算的。

Ambiguity Elimination

A compiler cannot use an ambiguous grammar because each input program must be parsed to a unique parse tree to show the structure.

To remove ambiguity in a grammar, we can transform it by hand into an unambiguous grammar. This method is possible in theory but not widely used in practical because of the difficulty.

Most compilers use additional information to avoid ambiguity.

CFG VS Regular expressions

Feature	Context-Free Grammar $(CFG)$	Regular Expression $(RE)$
Expressive Power	Can handle nested/recursive structures	Cannot handle nested structures
Grammar Structure	Production rules with non-terminals	Concatenation, union, Kleene star
Applications	Programming language syntax, parsing	Lexical analysis, simple text matching
Recognizer	Pushdown Automaton (PDA)	Finite Automaton (DFA/NFA)
Example Language	Balanced parentheses	Simple keywords, identifiers

Limit of CFG

• To prove a language is not context-free, you need pumping lemma for context free languages.

• To powerup the CFG/PDA, we can try again to add another stack to the machine, same as what we did to finite automata.

• This upgrade is ultimate. A finite automata with two stacks is as powerful as a Turing machine, which is the most powerful computational model that human can implement right now.

[[07-TOC-PDA|Pushdown Automata]]

Intuitively, a PDA is a finite automata plus a stack with some modifications on the transitions to fit stack behaviors.

• An NPDA is (formally) a 6-tuple $(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,F)$, where
  • $Q$ is a finite set of states,
  • $\mathrm{\Sigma }$ is a finite set of the input alphabet,
  • $\mathrm{\Gamma }$ is a finite set of the stack alphabet,
  • $\delta :Q\times {\mathrm{\Sigma }}_{ϵ}\times {\mathrm{\Gamma }}_{ϵ}\to \mathcal{P}(Q\times {\mathrm{\Gamma }}_{ϵ})$ is the transition function,
  • $q_0\in Q$ is the start state, and
  • $F\subseteq Q$ is the set of accept states.

For example, the context-free language $L=\{0^n{1}^n|n\ge 0\}$ has grammar

$$E\to 0E1|ϵ$$

Top-Down Parsing

Parser

• Now, we want to implement a parser which

  • takes a sequence of tokens as input;
  • analyze the structure of the input;
  • generates a parse tree; and
  • indicates the syntax errors if there is any.

• There are two types of parsers:

  • top-down
  • bottom-up.

Top-down parsing tries to construct a sequence of tokens from the grammar which is same as the input. Bottom-up parsing tries to match the input tokens with grammar rules.

Top-down Parsing

Top-down parsing is only for a subset of context-free grammars.

• Top-down parsing means that we generate the parse tree from top to bottom.

• Remember that the internal vertices in a parse tree are the nonterminals (variables), while the leaves are the terminals (tokens).

• The parse tree construction depends on the production rules in the grammar.

• If we want to construct the parse tree from top to bottom, the production rules have to be nicely designed.

Leftmost derivation

The RHS of each production rule always starts from a different terminal. The parsing on the left branch always finishes before the right branch.

For example, the following grammar parses single variable declarations (if we do not care about types here).

$$L\to idT$$$$T\to ;$$

Suppose the input is $id;$. The input tokens can be uniquely parsed into

Recursive-Descent Parser

However, our life cannot be that easy in most of cases.

• The previous grammar does not allow multiple variable declarations in one statement.

So, consider this grammar.

$$L\to id;$$$$L\to id,L$$

and try to parse $id,id,id;$

We have two different choices for the first derivation.

$$L\Rightarrow id;orL\Rightarrow id,L$$

We cannot decide which production rule can be used for the derivation. The parser will pick a valid rule randomly.

If the guess is wrong, the parser cannot proceed parsing on some input tokens and it will backtrack.

Actually, you have seen backtracking in other places … Depth First Search.

We can express the parsing by using a DFS tree.

• Each vertex in the tree is a valid sentential form (a stream of terminals and nonterminals). In this example, the stream to the RHS of $\Rightarrow$ , given by a step number $S_i$.
• Each edge is defined by applying a production rule.

The minor difference here is that we don’t need to go back to the root (as DFS) when the parsing is finished.

Note that this DFS is different from the parse tree because a vertex presents a sentential form, which is equivalent to a (partial) parse tree.

Each nonterminal $A$ is implemented by an individual function.

• Iterate on every rule starts with $A$ on LHS.
• Remember to resume the tokens when derivation fails.

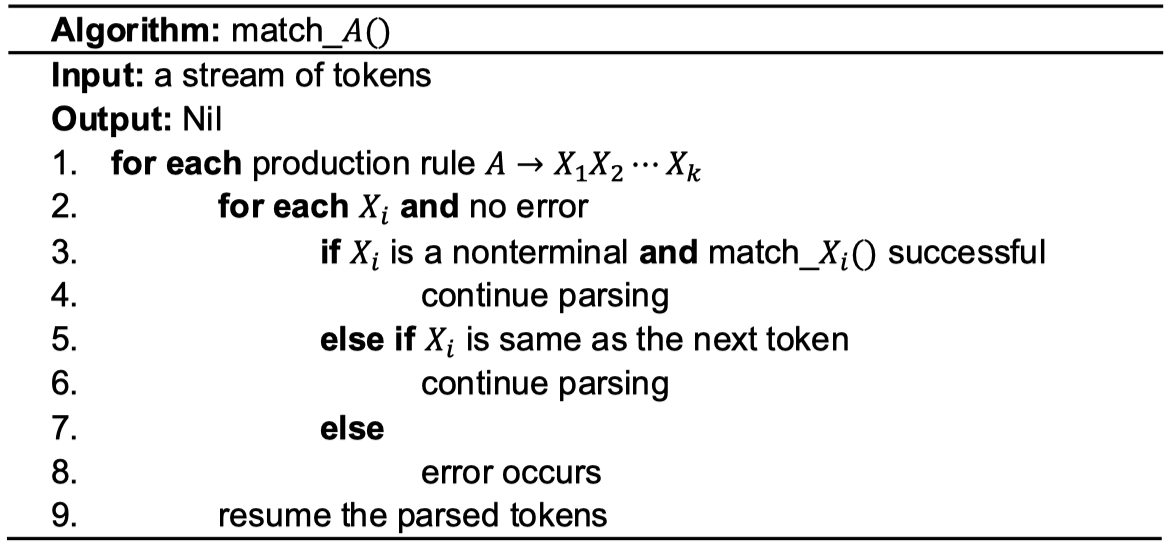
The parse tree generation can be done at Row 4 and Row 6, when the algorithm continues parsing.

You can also record the derivation rules and generate the parse tree when parsing is finished.

Resuming the parsed tokens at Row 9 can be implemented by a stack. When a token is matched with a terminal, push the token into the stack. When error occurs, we pop the tokens and put them back to the input.

The main routine starts from matching the start variable.

The parser reports syntax error when the main routine has tried all possible production rules. A syntax error can be

• the parser receives a token which cannot be parsed;
• after processing all tokens, the parse is incomplete (some leaves are nonterminals); or
• when the parsing is complete (all leaves are terminals), there are some tokens remained in the input.

Disadvantages of Recursive-Descent Parser

• The implementation (in code) can be very complicated/ugly because it needs to try many production rules, imaging many try-catch scopes nested with each other.
• It waste a lot of time on backtracking.
• It needs additional space to store the tokens for resuming purpose.
• In practical, nobody uses recursive descent parser.

$LL(1)$ Grammar

Predictive Parser

To avoid backtracking, we want to design a parser which can guess the next token from the input.

A correct guess can let the parser uniquely choose a production rule for parsing.

The idea is using a temporary space to store some tokens in advanced, like a buffer. Then, use the buffered tokens to make decisions.

This technique is very similar to space-time trade-off in the dynamic programming, what we have learned in algorithms.

The time complexity of recursions with backtracking can go up to $O(2^n)$.

But, if we can choose rules uniquely, the time complexity becomes $O(n)$.

$LL(1)$

Consider the grammar

$$L\to idT$$$$T\to ,idT$$$$T\to ;$$

which is equivalent to the above one and try to parse $id,id,id;$

• In the first iteration, the parser has to use the rule $L\to idT$.

• In the second iteration, there are two production rules "$T\to ,idT$" or "$T\to ;$ "

• This uncertainty can be easily solved by just “looking” at the next token from the lexer. This token is called lookahead token.

• Normally, when lexer returns a token to parser, the token is consumed. But the lookahead token remains in the input.

• The lookahead token in this example is "$,$ ". So, the parser knows the rule is $T\to ,idT$.

Because the parser reads tokens from left to right, does leftmost derivation, and looks at most one lookahead token(could not be a non-terminal); this parser/grammar is called $LL(1)$ .

Some grammars may not be $LL(q)$ .

• For example, the one we have seen.

$$L\to id;|id,L$$

• Looking one token ahead is insufficient for this grammar.

• $L\to id$ ; and $L\to id$ , $L$ agree on the first token.

• If the lookahead token is “$id$”, we cannot decide which rule will be used. Thus, to parse this grammar without recursions, the parser needs to look 2 tokens ahead.

  • This is $L(2)$ grammar.

In general, we can design $LL(k)$ grammar, for constant $k$.

In practical, more lookahead tokens make no big differences but increase the implementation difficulties.

More importantly, $LL(1)$ grammar is already powerful enough.

Left factoring

Left-factoring is a grammar transformation to convert a grammar to $LL(1)$ .

Back to the example,

$$L\to id;|id,L$$

is not $LL(1)$ because the first token of the two rules are the same. One lookahead token is not enough to the two productions.

We can solve this issue by introducing a new nonterminal $L^{\prime }$. 提取相同的token

And convert the grammar to

$$L\to id{L}^{\prime }$$$$L^{\prime }\to ;|,L$$

The new grammar is $LL(1)$, which is equivalent to

$$L\to idT$$$$T\to ,idT|;$$

This conversion is called left-factoring.

More formally, for each nonterminal $A$ which has multiple productions starting with the same prefix $\alpha$:

$$A\to \alpha {\beta }_1|\alpha {\beta }_2|\dots |\alpha {\beta }_k|{\gamma }_1|\dots |{\gamma }_n$$

where $\alpha$ is a non-empty sequence of grammar symbols (terminals and nonterminals), ${\beta }_1,\dots ,{\beta }_k$ and ${\gamma }_1,\dots ,{\gamma }_n$ are (possibly empty) sequences of grammar symbols.

Create a new nonterminal $A^{\prime }$ and transform the rules as

$$A\to \alpha A^{\prime }|{\gamma }_1|\dots |{\gamma }_n$$$$A^{\prime }\to {\beta }_1|\dots |{\beta }_k$$

Left Recursion Elimination

Some grammars are not good enough even after left factoring.

• For example, again to parse the variable declaration

$$L\to A;$$$$A\to id|A,id$$

• No production rule has a same prefix on RHS. But lookahead tokens do not work.

Suppose, the parser at some point needs to derive the nonterminal $A$.

One may try: if the lookahead token is $id$, the parser uses $A\to id$ If the lookahead token is $A$, it uses $A\to A,id$.

Be careful! $A$ is a nonterminal but not a token. A lexer can never find such a lookahead token.

As a result, $A\to A$ , $id$ will never be used. Obviously, this is wrong.

The problem is cause by $A\to A,id$. The RHS starts from a nonterminal, which cannot be used to match with a lookahead token.

This type of grammar is called left recursive.

Note that this still left-most derivation. Left-most or right-most derivation is not related to grammar itself. It only relates to in which order we derive the nonterminals.

Formally, a left recursive grammar has a valid derivation $A\stackrel{\ast }{\Rightarrow }A\alpha$ , where $A$ is a nonterminal and $\alpha$ is a string of grammar symbols.

In general, a left recursive production rule has the form

$$A\to A\alpha |\beta$$

This production can be derive $\beta ,\beta \alpha ,\beta \alpha \alpha \dots$

The parsing stops at $A\to \beta$ , and can produce as many $\alpha$ as possible.

So, we can let $A$ derives $\beta$ first and followed by some $\alpha$.

$$A\to \beta A^{\prime }$$$$A^{\prime }\to \alpha A^{\prime }|ϵ$$

Note that the production from $A^{\prime }$ can be $A^{\prime }\to \alpha A^{\prime }|\alpha$ But this is not $LL(1)$

Formally, for each nonterminal $A$ which has one or more productions with RHSs starting with the same nonterminal $A$:

$$A\to A{\alpha }_1|A{\alpha }_2|\dots |A{\alpha }_k|{\beta }_1|\dots |{\beta }_n$$

where ${\alpha }_1,\dots ,{\alpha }_k$ and ${\beta }_1,\dots ,{\beta }_n$ are (possibly empty) sequences of grammar symbols.

Create a new nonterminal $A^{\prime }$ and transform the grammar as

$$A\to {\beta }_1{A}^{\prime }|\dots |{\beta }_n{A}^{\prime }$$$$A^{\prime }\to {\alpha }_1{A}^{\prime }|\dots |{\alpha }_k{A}^{\prime }|ϵ$$

Exercise

Given the following grammar, try to do left factoring and eliminate left recursions.

$$E\to E+T|E-T|T$$$$T\to id|(E)$$

---

Ans:

$$E\to T{E}^{\prime }$$$$E^{\prime }\to +T{E}^{\prime }|-T{E}^{\prime }|ϵ$$$$T\to id|(E)$$

---

Limitations

In the last example, the grammar is left associative before conversion, but becomes right associative after conversion.

This totally changes the structure of the parse tree for some expressions, like “$id-id-id$".

In fact, top-down parsing cannot solve this issue. We need to either use a bottom-up parser or be stuck into the implementation details.

There are also some unambiguous context-free grammar cannot be converted into $LL(1)$ even after doing left factoring and left recursion elimination.

• For example, the one we used to show ambiguity elimination

$$S\to M|U$$$$M\to if(E)MelseM|other$$$$U\to if(E)S|if(E)MelseU$$

After left factoring $U$ becomes

$$U\to if(E)U^{\prime }$$$$U^{\prime }\to S|MelseU$$

Here are some last words about (recursive) predictive parsers.

• A predictive parser can always correctly predict what it has to do next.
• Predictive parsers can always be implemented by a recursive parser without using lookahead tokens.
• Without further specification, we consider recursive parsers and predictive parsers are the same.
• One major disadvantages of (recursive) predictive parsers is that they are not very efficient in implementations. Each production rule is implemented as a function. The parser needs to make many function calls and returns, which consume a lot of resources.

To avoid the function calls, we introduce nonrecursive predictive parsers.

Non-recursive Parser

To avoid recursions, we introduce non-recursive predictive parsers.

Intuitively, predictions are required when a nonterminal has multiple production rules.

The predictions are based on the next token. One token is enough because we are parsing $LL(1)$ grammars.

However, this method has troubles when the RHS of some rules start with nonterminals.

• For example

$$A\to B|C$$$$B\to b$$$$C\to c$$

• We cannot decide whether we are going to use $A\to B$ or 𝐴 without looking at $B\to b$ and $C\to c$.

Thus, we can "preprocess" the grammar to find the first tokens derived by each nonterminal before parsing the tokens.

The result of preprocessing is presented by a table, called parsing table. The rows are the nonterminals and the columns are terminals. The entry $M[A,\alpha ]$ is a production rule $A\to \alpha$ meaning that if the input token is $\alpha$, we will apply the rule $A\to \alpha$. The parser can parse the input tokens by checking the parsing table and using a stack.

This method is similar to the push-down automata but presented differently.

• Initially, push $ and $E$ into the stack ($E$ on top of $ ) where $E$ is the first nonterminal. Also insert $ to the end of the input stream of tokens.

Parsing using a parsing table

• In each iteration,

  • Assume the next input token is $\alpha$;
  • Pop the first item from the stack denoted by $X$;
  • If $X$ is a terminal, then try to match it with the next input token $\alpha$;
  • If $X$ is a nonterminal, then $M[X,\alpha ]$ in the parsing table is a production rule, denoted by $X\to \alpha$. Then, push everything in $\alpha$ to stack from right to left.

• When the stack pops $ and all input tokens are consumed, the parsing halts.

• $ is an artificial token, means the end of the stream.

Example

Given the parsing table and try to parse

$$(id+id)\ast id$$

	id	+	*	(	)	$
E	E → TE′			E → TE′
E′		E′ → +TE′			E′ → ε	E′ → ε
T	T → FT′			T → FT′
T′		T′ → ε	T′ → *FT′		T′ → ε	T′ → ε
F	F → id			F → (E)

Production Rule	Input	Stack	Pop
	(id + id) * id $	$E
$E\to T{E}^{\prime }$	(id + id) * id $	$E'T	$E$
$T\to F{T}^{\prime }$	(id + id) * id $	$E'T'F	$T$
$F\to (E)$	(id + id) * id $	$E'T')E(	$F$
Token Matched	id + id) * id $	$E'T')E	$($
$E\to T{E}^{\prime }$	id + id) * id $	$E'T')E'T	$E
$T\to F{T}^{\prime }$	id + id) * id $	$E'T')E'T'F	$T
$F\to id$	id + id) * id $	$E'T')E'T'id	$F
Token Matched	+ id)** * id $	$E'T')E'T'	$id$
$T^{\prime }\to \epsilon$	+ id) * id $	$E'T')E'	$T^{\prime }$
$E^{\prime }\to +T{E}^{\prime }$	+ id) * id $	$E'T')E'T+	$E^{\prime }$
Token Matched	id) * id $	$E'T')E'T	$+$
$T\to F{T}^{\prime }$	id ) * id $	$E'T')E'T'F	$T$
$F\to id$	id ) * id $	$E'T')E'T'id	$F$
Token Matched	) * id $	$E'T')E'T'	$id$
$T^{\prime }\to \epsilon$	) * id $	$E'T')E'	$T^{\prime }$
$E^{\prime }\to \epsilon$	) * id $	$E'T'	$E^{\prime }$
Token Matched	) * id $	$E'T'	$)$
$T^{\prime }\to \ast F{T}^{\prime }$	* id $	$E'T'F*	$T^{\prime }$
Token Matched	id $	$E'T'F	$\ast$
$F\to id$	id $	$E'T'id	$F$
Token Matched	$	$E'T'	$id$
$T^{\prime }\to \epsilon$	$	$E'T	$T^{\prime }$
$E^{\prime }\to \epsilon$	$	$E	$E^{\prime }$
Token Matched	$		$\mathrm{\$}$

Some entries $M[A,\alpha ]$ in the parsing table are empty.

Meaning that id you try to parse the token $\alpha$ by a nonterminal $A$, the parser returns an error message.

For example, assume the input tokens are $id+\ast idid$, the parsing will be stuck somewhere in the middle.

The error handling will be discussed at the end.

Intuitively, a parsing table enumerates all possible tokens can be derived by a nonterminal.

When a parser reads a token from input, it has a unique production rule to apply.

Thus, we need to analyze the grammar and find the prefix (the first token) of all possible sentential form derived by each nonterminal.

First

By putting all the firstly produced tokens into a set, we defined $First()$ .

• For example,

$$E\to E+T|E-T|T$$$$T\to id|(E)$$

• $id\in First(T)$ because $T\Rightarrow id$
• $(\in First(T)$ because $T(E)$.
• $id\in First(E)$ because $E\Rightarrow T\Rightarrow id$.
• $(\in First(E)$ because $E\Rightarrow R\Rightarrow (E)$.

Formally, $First(X)$ for each grammar symbol is computed by

Note: each $Y_i$ on line 3-5 can be either a terminal or a nonterminal.

Follow

When a terminal produces $ϵ$, things get complicated.

• For example,

$$A\to BC$$$$B\to bB|ϵ$$$$C\to c$$

• The parser need to use the rule $B\to ϵ$ to parse $c$.

However, $ϵ$ is not an input token which can be used for making predictions.

To handle this case, we also define $Follow(E)$, the next token possibly derived by some rules after $E$.

• In this example, $c\in Follow(B)$ because $A\Rightarrow BC\Rightarrow Bc$.

• When the parser receives $c$ as the next token, it knows $B\to ϵ$ is the correct rule.

Parsing Table Construction

Recall the parsing table $M$ is $n\times m$, where $n$ is the number of nonterminals and $m$ is the number of terminals.

The entry $M[A,\alpha ]$ is a production rule that the parser will apply when the current nonterminal is 𝐴 and the next token is $\alpha$.

For each production $A\to \alpha$ in the (left factored, non-left recursive) grammar, do the following:

1. For each token $\alpha$ in $First(\alpha )$, add the grammar production $A\to \alpha$ to $M[A,\alpha ]$
2. If $ϵ\in First(\alpha )$, then for each token $b$ in $Follow(A)$, add $A\to \alpha$ to $M[A,b]$
3. All other entries in the table are left blank and correspond to a syntax error.

Note that Rule 2 is applied when $\alpha$ is $ϵ$ because $ϵ$ is in $First(ϵ)$.

To create a parsing table for a non-recursive parser,

• eliminate any ambiguity from the grammar,
• eliminate left recursion from the grammar,
• left factor the grammar,
• compute the $First$ sets for all tokens and nonterminals,
• compute the $Follow$ sets for all nonterminals, and
• use those $First$ and $Follow$ sets to construct the parsing table.

Bottom-Up Parsing

Limit of Top-Down Parsing

Back to the example in Top-Down Parsing. The following grammar is left-recursive.

$$E\to E-T|T$$$$T\to id$$

Thus, top-down parsing needs to eliminate left recursion first.

$$E\to T{E}^{\prime }$$$$E^{\prime }\to -T{E}^{\prime }|ϵ$$$$T\to id$$

However, the conversion changes the structure of some sentences, like $id-id-id$.

Bottom-Up Parsing

Bottom-up parsing is more natural to human.

Think about how we analyze the arithmetic expressions. First, we calculate the subexpression in parentheses or the operator of the highest precedence. Then, the intermediate result will involve in the following calculations. The procedure is not from left to right.

Same thing happens when we analyze sentences in a program.

To the parse tree construction, the bottom-up procedure starts from isolated leaves, merges some of them to form a subtree, and eventually constructs the entire tree by placing a root.

The parse tree generated by bottom-up has no difference with by top-down, the internal vertices are nonterminals and leaves are tokens.

In fact, you have seen the similar procedure in Algorithm – the construction of Huffman code.

Because the bottom-up parsing is an inverse of top-down paring, the basic strategy is to use the LHS of some production rules to replace the RHS after reading some input tokens.

Thus, in the bottom-up parsing, there are two basic operations.

• Shift
  • The parser needs to read more tokens from the input.
  • The tokens have already read are insufficient for any production rule.
• Reduce
  • The parser has already read enough tokens.
  • It can replace the RHS by the LHS of some production rules.

The parser is called shift-reduce parser.

The parser also needs a stack to hold the tokens which are read but not consumed (reduced) yet.

Example of Bottom-Up Parsing

• Let’s look at a small example first. Given the following grammar and try to parse $abbcbcde$.

$$S\to aABe$$$$A\to Abc$$$$A\to b$$$$B\to d$$

No.	Stack	Input	Output
0		abbcbcde
1	a	bbcbcde	shift
2	ab	bcbcde	shift
3	aA	bcbcde	reduce using A → b
4	aAb	cbcde	shift
5	aAbc	bcde	shift
6	aA	bcde	reduce using A → Abc
7	aAb	cde	shift
8	aAbc	de	shift
9	aA	de	reduce using A → Abc
10	aAd	e	shift
11	aAB	e	reduce using B → d
12	aABe		shift
13	S		reduce using S → aABe

The above example shows how bottom-up parsing works on a small instance.

However, to formally define a bottom-up parser, we need to generalize this procedure to all grammars. Many details will be discussed.

Even within this small example, careful reader may find the above procedure has some problems. In Step2, we read b. Then, we immediately reduce 𝑏 to A in Step3. But the thing is different in Step4. We read b again, but the parser waits until it reads another c and reduces Abc to A.

In general, similar to the predictive parser, there might be multiple options in bottom-up parsing. We need to clearly define which option is used under a certain condition.

LR Parsing Algorithm

LR Parser

There are many different ways to solve the above problem, like using recursions (Same as what we did in the predictive parsing, recursions simply enumerate all possible options.)

In this course, we only introduce $LR(k)$ parsers (k lookahead tokens, LR parser for short) because

• $LR(k)$ parsers can be used to almost all (but not all) context-free grammars.
• They are the most powerful non-backtracking shift-reduce parsers;
• they can be implemented very efficiently; and
• they are strictly more powerful than $LL(k)$ grammars.

When a reduction is performed, the $RHS$ of the production rule is already on the stack, which is some additional information to help decision making.

The parser puts state symbols into the stack to speedup checking the content on the stack.

Imaging that you want to check what’s on the given stack. You need to pop everything out, see if the content is same as what you want, then push everything back. This is very inefficient.

Thus, we use a state symbol to indicate the current content on the stack.

This symbol is called state symbol because it is exactly same the states in a DFA.

We can consider each state in a DFA means that "To reach this state, the input must be some specific strings."

Also, each $X_i$ is corresponds to an $S_i$, like a pair.

To parse a $LR$ grammar, you are also given a parsing table. This parsing table again enumerates the actions the parser needs to take in all possible situations.

Each row in the table represents a state in PDA. The columns are split into two individual fields: ACTION and GOTO.

• Each column in ACTION represents a terminal.
• Each column in GOTO represents a nonterminal.
• The value of the entry ACTION $[S_m,a_i]$ shows the action taken by the parser when the current state is $S_m$ and the input token is $a_i$
• The value are of two types:
  • $Shift{S}_i$ , meaning that the parser pushes the next input token into the stack and move to the state $S_i$;
  • $Reduce{R}_i$, meaning that the parser reduces some (non)terminals using the production rule $r_i$.
• The value of the entry $GOTO[S_m,A]$ is a state symbol, $S$ for example, meaning that the parser goes to the state $S$ after it reduces the stack uses a production rule $A\to \beta$, for some $\beta$.

[!abstract]+ LR Parsing Algorithm

1. Put the special symbol $ at the end of the input.
2. Put state 0 at the bottom of the stack.
3. In each iteration, suppose the current configuration is $<0\underset{―}{X_1{S}_1}\dots \underset{―}{X_m{S}_m}{a}_i\dots a_n\mathrm{\$}>$, the current state is $S_m$, and the next input token is $a_i$.

• If $ACTION[S_m,a_i]$ is "shift S", then the next configuration is $<0\underset{―}{X_1{S}_1}\dots \underset{―}{X_m{S}_m}\underset{―}{a_{i}S}\dots a_n\mathrm{\$}>$.
• If $ACTION[S_m,a_i]$ is "reduce $A\to B$", then the next configuration is $<0\underset{―}{X_1{S}_1}\dots \underset{―}{X_{m-r}{S}_{m-r}}\underset{―}{AS}\dots a_n\mathrm{\$}>$, where $r=|\beta |$ and $S=GOTO[S_{m-r},A]$. At the same time, the parser outputs $A\to \beta$.
• If $ACTION$ $[S_m,a_i]$ is "accept" and the current configuration is $<0X{S}_1>$ , where $X$ is the start symbol of the grammar, the parser accepts the input.
• For all other cases, like $ACTION$ $[S_m,a_i]$ is blank, the parser finds a syntax error and switch to error recovery.

Example

State	id	+	*	(	)	$	E	T	F
0	s5			s4			1	2	3
1		s6				acc
2		r2	s7		r2	r2
3		r4	r4		r4	r4
4	s5			s4			8	2	3
5		r6	r6		r6	r6
6	s5			s4			9	3
7	s5			s4			10
8		s6			s11
9		r1	s7		r1	r1
10		r3	r3		r3	r3
11		r5	r5		r5	r5

Stack	Input	Output
0	id + id * id$
0id 5	+ id * id$	shift 5
0F 3	+ id * id$	reduce F → id
0T 2	+ id * id$	reduce T → F
0E 1	+ id * id$	reduce E → T
0E 1 + 6	id * id$	shift 6
0E 1 + 6 id 5	* id$	shift 5
0E 1 + 6 F 3	* id$	reduce F → id
0E 1 + 6 T 9	* id$	reduce T → F
0E 1 + 6 T 9 * 7	id$	shift 7
0E 1 + 6 T 9 * 7 id 5	$	shift 5
0E 1 + 6 T 9 * 7 F 10	$	reduce F → id
0E 1 + 6 T 9	$	reduce T → T * F
0E 1	$	reduce E → E + T
0E 1	$	accept

SLR Parsing

Previously, we have introduced the $LR$ parsing algorithm using the parsing table. Now, the question is how to construct a parsing table for a given context-free grammar.

In fact, there are many ways to construct a parsing table for different 𝐿𝑅 parsers:

$LR(0)$, $SLR(1)$,$LALR(1)$, $LR(1)$ etc. (by increasing power).

For $LR(k)$ with $k\ge 2$ are not used in practice because of the complexity.

We will focus on $SLR(1)$ (simple $LR$), then move on to $LR(0)$, $LALR(1)$ , and $LR(1)$ .

SLR Parser

To construct an $SLR$ parsing table, we do three things

• augment the context-free grammar;
• construct a DFA based on the computation of set of items;
• represent the DFA using the transition table;

The construction in $Step2$ is very similar to transforming an NFA to a DFA, except that it will be based on sets of items of the same behavior instead of sets of NFA states.

Augmented Grammar

Given a grammar with a start symbol $S$.

$$S\to \dots$$$$\cdots \to \dots$$

we construct the corresponding augmented grammar by artificially introducing a nonterminal $S^{\prime }$ and a production rule.

$$S^{\prime }\to S$$$$S\to \dots$$$$\cdots \to \dots$$

This artificial production rule seems to be useless, but it guarantees that the parser accepts the input when it reduces using $S^{\prime }\to S$.

$LR(0)$ items

The $LR(0)$ items are originally defined for $LR(0)$ parser, but do the same thing in $SLR(1)$ .

An $LR(0)$ item (item, for short)is simply a grammar production with a dot somewhere in its RHS.

• For example, the production $A\to XYZ$ can create 4 items

$$A\to \cdot XYZ$$$$A\to X\cdot YZ$$$$A\to XY\cdot Z$$$$A\to XYZ\cdot$$

As a special case, the production $A\to ϵ$ only generates $A\to \cdot$

Each item represents a state that the parser is currently in. If the parser is in the state corresponding to $A\to X\cdot YZ$, it means the parser has already push $X$ into the stack and expects to match $YZ$ from the input.

If $Y$ is a nonterminal and the grammar also has a production $Y\to UVW$, then the parser also expects to see $UVW$.

Thus, the parser state corresponds to $A$ correspond $Y\to \cdot UVW$.

Closure of items

Keep this intuition in mind, we find the closure of a set of items $I$ recursively using the following algorithm.

• Every item in $I$ is in $closure(I)$.

• If $A\to \alpha \cdot B\beta$ is an item in $closure(I)$ and if $B\to \gamma$ is a production, where $A$ and $B$ are nonterminals and $\alpha$, $\beta$ , and $\gamma$ are any sequence of terminals and nonterminals, then add the item $B\to \cdot \gamma$ to $closure(I)$.

• Repeat the above two steps until $closure(I)$ does not change.

• For example,

$$E^{\prime }\to EE\to E+T|T$$$$T\to T\ast F|FF\to (E)|id$$

$closure(\{E^{\prime }\to E\})=$

$$\{E^{\prime }\to \cdot E,E\to \cdot E+T,E\to \cdot T$$$$T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$$

Goto Function

Then, we define $goto$ function.

For all the items of the form $A\to \alpha \cdot X\beta$ in a set of items $I$, where $X$ is an arbitrary grammar symbol (token or nonterminal), we define $goto(I,X)$ as the closure of the set of items of the form $A\to \alpha X\cdot \beta$.

• For example, given the set of items $I=\{E^{\prime }\to E\cdot ,E\to E\cdot +T\}$, to find $goto(I,+)$:

  • the item $E^{\prime }\to E\cdot$ does not create any new item by taking "+";
  • the item $E^{\prime }\to E\cdot +T$ implies the new item $E\to E+\cdot T$

• Thus,

$$goto(I,x)=closure(\{E\to E+\cdot T\})$$$$=\{E\to E+\cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$$

更新时，当一个token 时non-terminal 时，继续传递

Set of items

Set of items construction algorithm

Next, we construct the DFA to decide the tokens in the stack. This method is called set-of-items construction algorithm. Each set of items $I_i$ represents a state in the DFA.

1. Compute $I_0=closure(\{S^{\prime }\to \cdot S\})$ and add the unmarked $I_0$ to $S_D$, where $S^{\prime }$ is the start symbol of the augmented grammar and $S_D$ is the set of DFA states.
2. While there is an unmarked DFA state $I_i\in S_D$, do the following:
   1. For each grammar symbol $X$, do the following:
      1. Compute the DFA state $I_j=goto(I_i,X)$.
      2. If $I_j\ne \mathrm{\varnothing }$ and $I_j\ne \in S_D$ then add the unmarked $I_j$ to $S_D$.
      3. If $I_j\ne \mathrm{\varnothing }$ then define $mov{e}_D(I_i,X)=I_j$.
   2. Mark $I_i$ in $S_D$.

Example

For example,

$$E^{\prime }\to EE\to E+T|T$$$$T\to T\ast FF\to (E)|id$$

Initially, $I_0=closure(\{E^{\prime }\to E\})$

$$=\{E^{\prime }\to \cdot E,E\to \cdot E+T,E\to \cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$$

Then, we consider the $goto$ function from $I_0$ by taking each grammar symbol.

• For $goto(I_0,E)$:

Production	Goto Symbol: $E$
$E^{\prime }\to \cdot E$	$E^{\prime }\to E\cdot$
$E\to \cdot E+T$	$E\to E\cdot +T$
$E\to \cdot T$	$\mathrm{\varnothing }$
$T\to \cdot T\ast F$	$\mathrm{\varnothing }$
$T\to \cdot F$	$\mathrm{\varnothing }$
$F\to \cdot (E)$	$\mathrm{\varnothing }$
$F\to \cdot id$	$\mathrm{\varnothing }$

Thus, $goto(I_0,E)=closure(\{E^{\prime }\to E\cdot ,E\to E\cdot +T\})$

• $=\{E^{\prime }\to E\cdot ,E\to E\cdot +T\}=I_1$

Similarly,

• $\text{goto}(I_0,T)=\text{closure}(\{E\to T\cdot ,T\to T\cdot \ast F\})=\{E\to T\cdot ,T\to T\cdot \ast F\}=I_2$
• $\text{goto}(I_0,F)=\text{closure}(\{T\to F\cdot \})=\{T\to F\cdot \}=I_3$
• $\text{goto}(I_0,()=\text{closure}(\{F\to (\cdot E)\})=\{F\to (\cdot E),E\to \cdot E+T,E\to \cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}=I_4$
• $\text{goto}(I_0,id)=\text{closure}(\{F\to id\cdot \})=\{F\to id\cdot \}=I_5$
• $\text{goto}(I_0,E^{\prime })=\text{goto}(I_0,+)=\text{goto}(I_0,\ast )=\text{goto}(I_0,))=\mathrm{\varnothing }$

[!example]+ DFA

In the following, $goto(I_i,X)=\mathrm{\varnothing }$ will be omitted for symbol $X$. Consider the $goto$ function for $I_1,I_2,I_3,I_4,I_5$

• $\text{goto}(I_1,+)=\text{closure}(\{E\to E+\cdot T\})=\{E\to E+\cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}=I_6$

---

• $\text{goto}(I_2,\ast )=\text{closure}(\{T\to T\ast \cdot F\})=\{T\to T\ast \cdot F,F\to \cdot (E),F\to \cdot id\}=I_7$

---

• $\text{goto}(I_4,E)=\text{closure}(\{F\to (\cdot E)\})=\{F\to (E\cdot ),E\to E\cdot +T\}=I_8$
• $\text{goto}(I_4,T)=\text{closure}(\{E\to \cdot T,T\to T\cdot \ast F\})=I_2$
• $\text{goto}(I_4,F)=\text{closure}(\{T\to F\cdot \})=I_3$
• $\text{goto}(I_4,()=\text{closure}(\{F\to (\cdot E)\})=I_4$
• $\text{goto}(I_4,id)=\text{closure}(\{F\to id\cdot \})=I_5$

---

• $\text{goto}(I_3,X)$ and $\text{goto}(I_5,X)$ are omitted because they are $\mathrm{\varnothing }$ for all $X$.

[!example]+ DFA

---

We continue computing the $\text{goto}$ function from new states:

• $\text{goto}(I_6,T)=\text{closure}(\{E\to E+T\cdot ,T\to T\cdot \ast F\})=\{E\to E+T\cdot ,T\to T\cdot \ast F\}=I_9$

• $\text{goto}(I_6,F)=\text{closure}(\{T\to F\cdot \})=\{T\to F\cdot \}=I_3$

• $\text{goto}(I_6,()=\text{closure}(\{F\to (\cdot E)\})=\{F\to (\cdot E)\}=I_4$

• $\text{goto}(I_6,id)=\text{closure}(\{F\to id\cdot \})=\{F\to id\cdot \}=I_5$

---

• $\text{goto}(I_7,F)=\text{closure}(\{T\to T\ast F\cdot \})=\{T\to T\ast F\cdot \}=I_{10}$

• $\text{goto}(I_7,()=\text{closure}(\{F\to (\cdot E)\})=\{F\to (\cdot E)\}=I_4$

• $\text{goto}(I_7,id)=\text{closure}(\{F\to id\cdot \})=\{F\to id\cdot \}=I_5$

---

• $\text{goto}(I_8,))=\text{closure}(\{F\to (E\cdot )\})=\{F\to (E)\cdot \}=I_{11}$

• $\text{goto}(I_8,+)=\text{closure}(\{E\to E+\cdot T\})=\{E\to E+\cdot T\}=I_6$

---

In the last iteration

• $goto(I_9,\ast )=closure(\{T\to T\ast \cdot F\})=I_7$

Here is the list of sets of items.

i	$I_i$
0	$\{E^{\prime }\to \cdot E,E\to \cdot E+T,E\to \cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$
1	$\{E^{\prime }\to E\cdot ,E\to E\cdot +T\}$
2	$\{E\to T\cdot ,T\to T\cdot \ast F\}$
3	$\{T\to F\cdot \}$
4	$\{F\to (\cdot E),E\to \cdot E+T,E\to \cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$
5	$\{F\to id\cdot \}$
6	$\{E\to E+\cdot T,T\to \cdot T\ast F,T\to \cdot F,F\to \cdot (E),F\to \cdot id\}$
7	$\{T\to T\ast \cdot F,F\to \cdot (E),F\to \cdot id\}$
8	$\{F\to (E)\cdot ,E\to E\cdot +T\}$
9	$\{E\to E+T\cdot ,T\to T\cdot \ast F\}$
10	$\{T\to T\ast F\cdot \}$
11	$\{F\to (E)\cdot \}$

Set of items construction algorithm

In the DFA we constructed above, we don’t need final states. Because we use states to show the content in the stack. And the stack is reduced if DFA reaches a final state. More interestingly, a state, together with the string to reach the state, form a pair in the configuration.

To SLR parsing table

$SLR(1)$ Parsing Table Construction

First, we construct the $ACTION$ part of a $SLR(1)$ parsing table.

• If $A\to \alpha \cdot \alpha \beta$ (where $\alpha$ is a token) is an item in the set of items $I_j$ and $goto(I_i,\alpha )=I_j$, then set $ACTION[i,\alpha ]$ to "shift j".
• If $A\to \alpha \cdot$ is an item in the set of items $I_i$, then set $ACTION[i,\alpha ]$ to "reduce $A\to \alpha$" for all $\alpha$ in $Follow(A)$.
• If $S^{\prime }\to S\cdot$ (where S' is the start symbol of the augmented grammar) is an item in the set of items $I_i$, then set $ACTION[i,\mathrm{\$}]$ to accept.

For item 2, we give a number to each grammar production $A\to \alpha$ and put in the table "reduce" followed by the production's number.

Then, we construction the $GOTO$ part.

• If $goto(I_i,A)=I_j$, where $A$ is a nonterminal, then set $GOTO[i,A]$ to "$j$"

Summary

Here are the steps to create a parsing table for an $SLR(1)$ parser:

• Eliminate any ambiguity from the grammar.
  • Eliminate left recursion from the grammar.
  • Left factor the grammar.
• Augment the grammar with a new start symbol.
• Compute the sets of items for the grammar and build the corresponding DFA.
• Number the grammar productions.
• Compute the $First$ sets for all tokens and nonterminals.
• Compute the $Follow$ sets for all nonterminals.
• Use the sets of items, DFA, and the $Follow$ sets to construct the parsing table.

Other Bottom-Up Parsing

$LR(0)$ Parsing Table

$shift-reduce$ conflict

In fact, $SLR(1)$ cannot avoid $shift-reduce$ conflict entirely.

Consider the following ambiguous grammar.

$$S^{\prime }\to S,S\to L=R,S\to R,L\to \ast R,L\to id,R\to L$$

Construct the set of items

$$I_0=\{S^{\prime }\to \cdot S,S\to \cdot L=R,S\to \cdot R,L\to \cdot \ast R,L\to \cdot id,R\to \cdot L\}$$$$I_0\stackrel{S}{\to }{I}_{1}and{I}_1=\{S^{\prime }\to S\cdot \}$$$$I_0\stackrel{L}{\to }{I}_{2}and{I}_2=\{S\to L\cdot =R,R\to L\cdot \}$$$$I_2\stackrel{=}{\to }{I}_{3}and{I}_3=\{S\to L=\cdot R,R\to L\cdot ,L\cdot \ast R,L\to \cdot id\}$$

In addition, $FOLLOW(R)$ contains the token ‘ = ’.

Thus, the parsing table construction algorithm will put both = $shift$ and $reduce$ into the entry 𝐴𝐶𝑇𝐼𝑂𝑁 [2 , ] , which is conflict.

Sometimes, when current state is $I_2$, next token is "=", parser does not reduce $R\to L$

$$S^{\prime }\Rightarrow S\Rightarrow L=R\Rightarrow \cdot R=R\stackrel{R\to L}{\Rightarrow }\ast L=R$$$$S^{\prime }\Rightarrow S\Rightarrow L=R\Rightarrow id=R$$

---

To eliminate the conflict, we analyze the above grammar.

Then, we can see reduce(R → L) is not supposed to be performed in all the cases when the next input token is in FOLLOW(R).

• If L appears on the LHS of =, reduce(R → L) is only needed when there is a * before L.
• And if an L is on the RHS of =, this specific L can only be followed by $, but not =.

For example, if the input is * id = id, the parsing is as follows:

• · * id = id → shift
• * · id = id → shift
• * id · = id → shift
• * L · = id → reduce(L → id)
• * R · = id → reduce(R → L) (highlighted in red)
• L · = id → reduce(L → * R)
• L = · id → shift
• L = id · → shift
• L = L · → reduce(L → id)
• L = R · → reduce(L → R) (highlighted in red)
• S · → reduce(S → L = R)

$LR(1)$ Item

In addition to $LR(0)$ items, an $LR(1)$ item consists of an $LR(0)$ item and followed by a token.

For example, $A\to Z\cdot YZ,a$.

This additional token does not do anything in most cases.

Only for the items in the type $A\to X\cdot ,a$. The parser reduces the stack using the rule $A\to X$ only if the input token is $\alpha$.

Thus, $\alpha$ is a token in $FOLLOW(A)$.

For other tokens in $FOLLOW(A)$, the parser does not reduce.

Therefore, one state in the DFA for $LR(0)$ items is possibly split into multiple states in the DFA for $LR(1)$.

For the previous grammar, the state which has $R\to L\cdot$ is split into two states:

• one has $R\to L\cdot ,=$
• and the other has $R\to L\cdot ,\mathrm{\$}$

However, even the parsing table is upgraded in this way, some grammar can still create shift–reduce conflict.

Then, we can let each $LR(0)$ item be followed by a pair – the combination of two tokens, which results in an $LR(2)$ item using two lookahead tokens.

This upgrading process can continue and define an $LR(n)$ grammar, like $LL(n)$. But for this course, $LR(1)$ is enough, and we stop here.

$LALR(1)$ item

Instead of trying to solve more problems but creating chaos, sometimes we want to ignore some problems and keep our life easier. Thus, LALR(1) item is introduced.

Consider two $LR(1)$ items: $A\to X\cdot YZ,a$ and $A\to X\cdot YZ,b$.

• An $LALR(1)$ item merges these two items as $A\to X\cdot YZ,a|b$.
• This undoes the splitting from $SLR(1)$ to $LR(1)$.
• The merging reduces the number of states and loses very little power.

Back to the example, $R\to L,=|$$ is the LALR(1) item.